개발자로 후회없는 삶 살기
[22.02.11] 딥러닝 PART. 밑바닥부터 시작하는 딥러닝 발제 본문
서론
동아리에서 진행한 딥러닝 스터디의 발제 내용입니다.
※ 이 포스트는 다음 교재의 학습이 목적임을 밝힙니다.
- 저자
- 사이토 고키
- 출판
- 한빛미디어
- 출판일
- 2020.11.10
본론
- 신경망의 예

선형회귀 모델을 하나의 노드로 사용, 노드들이 원하는 깊이와 개수로 구성된 것입니다.
- 퍼셉트론의 원리와 h함수
4 ~ 0이면 0/ 1 ~ 5이면 1


-> 수식

1. 0 이하면 어떤 입력이든 0의 결과를 반환합니다.
2. w는 각 신호의 영향력을 나타냅니다.
3. b는 뉴런이 쉽게 활성화되는 것을 제어합니다.
4. 원래는 b 옆에도 w를 곱하는데 항상 1이라서 b만 표시합니다.
- 활성함수
1. 입력의 총합이 이 노드의 활성화를 일으킬 정도인지를 정합니다.
2. sigmoid

3. 비교 :
1) 활성함수로 계단 함수를 사용합니다.
2) 입력에 따라 출력이 연속적으로 변화 > 퍼셉트론 -> 조금 중요해도 1, 많이 중요해도 1
3) 계단 함수 코드

정수와 배열은 비교 대상이 성립이 안된다라는 오류가 발생합니다. ∴ 따라서 불린 인덱싱 방식을 활용하여 출력합니다.
4. 렐루

비선형 함수의 대표, 0과 양의 무한대를 표현합니다.
- 다차원 배열

1. 행렬 곱

2. 3층 신경망

-> 행렬 식

3. 최종 출력 모양 선택

- 출력층 설계
회귀 문제는 항등 함수, 분류 문제는 softmax
-> softmax 구현

sigmoid를 클래스 개수만큼 한 번에 적용하는 개념, 출력 층 뉴런 수 = 분류하고 싶은 클래스 수로 설정
- mnist
회색조의 1 채널 이미지 (컬러 이미지이면 3 채널 R, G, B)
-> 하이퍼파라미터
1. Normalization : 이미지의 경우 이미 0 ~ 255로 범위가 정해져 있습니다.
2. Flatten : 2차원 이미지를 1차원으로 펼칩니다.
3. One-hot encoding : label을 정수 vs 카테고리별 분류
=> 이미지 출력

정확도 코드

exp 지수함수의 무한대로 인해 over 되어서 정확도가 불안정한 모습입니다.
=> 배치 출력
위의 훈련된 걸 업로드한 w는 첫 번째 히든 레이어에 50개, 두 번째는 100이라고 임의로 지정합니다.

-> 100장의 샘플의 결괏값 출력
=> 배치 처리 결과

- 신경망 학습
=> 학습 발달 과정
1. 매개변수, 특징의 자동화
2. 사람의 수동 분석 및 지정 > 사람이 생각한 특징으로 기계가 학습 > 기계가 데이터로부터 특징까지 스스로 학습합니다.
3. Train vs Test : 훈련으로 최적의 매개변수를 찾고 시험으로 범용적인 모델 평가
- 손실함수
=> 오차제곱법

=> 크로스 엔트로피 오차


- 미니배치학습

-> 학습이란 손실 함수의 값을 구하고 그 값을 최대한 줄여주는 매개변수를 찾는 것입니다.
1. 이때 각 차원에 대한 loss를 구해야 하는데 이때 사용되는 데이터의 양에 기준입니다.
2. 한 개를 기준 vs 여러 개를 기준
-> 손실 함수를 사용하는 이유
1. cost함수의 점을 아주 조금 변화시켰을 때 손실 함수가 어떻게 변하나 관찰합니다.
2. 기울기가 양수 vs 음수 vs 0
-> 모델 학습의 지표를 정확도??
1. 계단 함수에 접목 : 미미한 변화에는 반응을 보이지 않음, 불연속적으로 변합니다.

2. 그래프의 모양 : 계단 함수는 미분이 0, 시그모이드는 곡선으로 미분이 0이 안 됩니다.
-> 설명 : gradient를 구할 때 로컬 gradient가 필요한데 그게 로컬에서 활성함수를 거쳐가므로 활성함수의 기울기가 표현됩니다.
+ : sigmoid도 0 ~ 1 사이의 값으로 인한 역전파시 경사 소실을 유발합니다.
- 수치미분

특정 순간의 변화량, 개선점 : h의 크기, 중심 차분

점 5, 10에서의 순간 변화량
- 편미분

인수가 여러 개인 미분
- gradient
한 점에서 모든 차원에 대한 기울기를 벡터로 정리한 것

모든 차원에 대한 기울기 -> 낮아지는 방향을 가리킵니다.
- 경사하강법
1. 학습 단계에서 손실 함수가 최솟값이 될 때의 매개변수를 찾는 방법 > 기울어진 방향이 반드시 최솟값은 아닙니다.
2. 수식

-> 내려가는 방향 * 학습률 만큼 이동합니다.
3. 코드


-> 결과 두 개의 차원일 때 극소점의 w 좌표가 나옵니다. > 학습률 조정 : 너무 크면 발산하고 vs 너무 작으면 고립됩니다.
- 신경망에서의 기울기

loss 함수에 대한 w의 기울기 : 조금 변경 시 L의 변화량

w -> 2 by 3
- 학습 알고리즘 구현
=> 순서
미니 batch 선별 > 기울기 산출 > 매개변수 갱신 > 최저점까지 반복 > 미니batch 학습

(전체 데이터 vs batch 사이즈의 데이터)를 써서 gradient를 구합니다.

지정 횟수만큼 반복합니다.
=> 평가

- 오차역전파
=> 그래프 이론
1. 원 안에 연산 내용 (+, ×)
2. 계산 결과는 화살표 위에
3. 계산은 왼쪽에서 오른쪽으로 진행
4. 순전파 : 결과가 오른쪽 끝에 도달하면 종료합니다.
5. 역전파 : 계산을 오른쪽에서 왼쪽 끝까지 진행
=> 국소적 계산
1. 해당 원의 일만 합니다.
2. 해당 원의 일이 뒤로 전달되어 복잡한 계산이 가능
=> 역전파에 의한 미분 값 전달

- 연쇄법칙

x : 전달된 계산 결과 ex) 200
f : 연산 내용 ex) × 2
y : 연산 결과
★ 연쇄 법칙 : 앞에서 온 신호에 국소적 미분 값을 곱해서 앞으로 전달
-> 국소적 미분 : 순전파 때 구함 + x에 대한 y의 미분

기억할 것 : 이 곱하기에 사용되는 건 전달받은 신호와 저장된 국소적 미분
- 연쇄법칙 계산

1. 앞의 신호 : 도함수 미분 값
2. 국소적 미분 값 : 순전파 과정에서 구해서 보관합니다.
3. 위의 수식 적용

x, y값은 주어지므로 x에 대한 z의 미분값은 스칼라 값으로 나옵니다.
- 역전파
1. 덧셈 노드 역전파
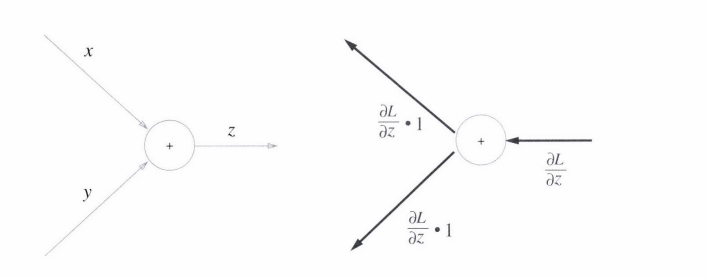
상류의 신호를 그대로 보냅니다.
2. 곱셈 노드 역전파

교차 전파
3. 풀어봅시다!

- 구현
=> 곱셈

-> 역전파 계산

=> 덧셈

=> 포인트

저장 및 보관에 용이합니다.
=> 렐루 계층

-> 활성함수의 기울기 개념 도입 (정확도의 성능 지표)
-> 코드


True인 요소만 0으로 변경
=> 시그모이드 계층

1) 흘러오는 신호 × 국소적 미분 값
2) 곱셈 계층과 덧셈 계층의 편리합니다.
3) 단순화

-> 입력과 출력에만 집중
=> 코드

간소화 버전
- Affine
=> 스칼라를 넘어서 행렬의 입력 버전

-> 행열의 형상에 주목
1. 1번 식을 구하기 Y에 대한 최종 결과의 미분 값은 Y 행렬과 동일한 모양, W 전치행렬 또한 (3 by 2) 모양을 변형한 (2 by 3) 모양이 나와야만 합니다.
2. 1번 식 -> 1×2 = (1×3) × (3×2)
=> 배치용 affine

항상 샘플 하나와 샘플 여러 개를 생각

오차 제곱합 구했을 때처럼 샘플 하나 vs 여러 개
- softmax 계층
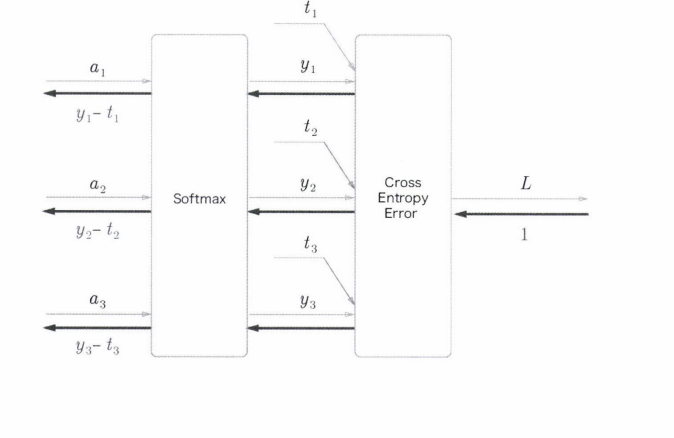
-> 3개의 입력
1. softmax로 인한 3개의 정규화 출력
2. loss 함수에서 예측값과 정답의 차이를 loss로 출력
3. 역전파의 결과 > 오차를 앞으로 전달하여 입력의 영향력 조절 목적
4. 오차 전달 방식
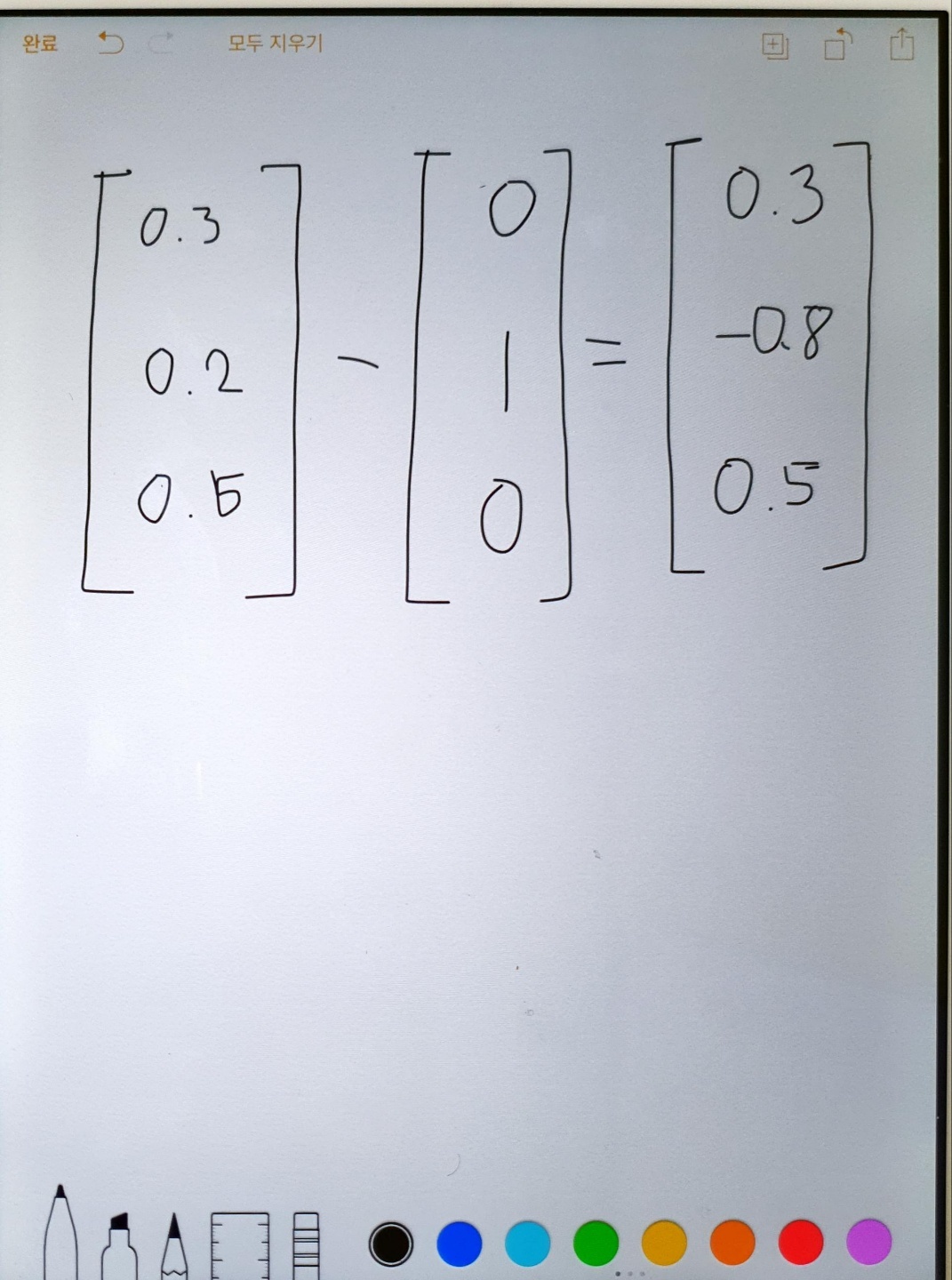
- 오차역전파 기울기 확인

'[AI] > [네이버 BoostCamp | 학습기록]' 카테고리의 다른 글
| [22.09.13] GAN PART.GAN 시스템 (0) | 2022.12.27 |
|---|---|
| [22.08.16] 딥러닝 PART.Batch Normalization (0) | 2022.12.27 |
| [22.04.27] 딥러닝 PART.CS231n 6강 (0) | 2022.12.27 |
| [22.01.19] 딥러닝 PART.CS231n 2강 (0) | 2022.12.27 |
| NLP PART.문장 유사도 (0) | 2022.12.26 |




