개발자로 후회없는 삶 살기
NLP PART.문장 유사도 본문
서론
※ 이 포스트는 다음 교재의 학습이 목적임을 밝힙니다.
https://wikidocs.net/book/2155
딥 러닝을 이용한 자연어 처리 입문
많은 분들의 피드백으로 수년간 보완된 입문자를 위한 딥 러닝 자연어 처리 교재 E-book입니다. 오프라인 출판물 기준으로 코드 포함 **약 1,000 페이지 이상의 분량*…
wikidocs.net
-> 전체 코드
GitHub - SangBeom-Hahn/NLP
Contribute to SangBeom-Hahn/NLP development by creating an account on GitHub.
github.com
본론
벡터의 유사도
문서의 유사도는 주로 문서들 간에 동일한 단어 또는 비슷한 단어가 얼마나 공통적으로 많이 사용되었는지에 의존합니다.
문서의 유사도의 성능은 각 문서의 단어들을 어떤 방법으로 수치화하여 표현했는지(DTM, Word2Vec 등), 문서 간의 단어들의 차이를 어떤 방법(유클리드 거리, cosine 유사도 등)으로 계산했는지에 달려있습니다.
1. cosine 유사도
단어를 수치화할 수 있는 방법을 이해했다면 이러한 표현 방법에 대해서 cosine 유사도를 이용하여 문서의 유사도를 구하는 게 가능합니다.
- 정의
두 벡터 간의 cosine 각도를 이용하여 구할 수 있는 두 벡터의 유사도를 의미합니다.
두 벡터의 방향이 완전히 동일한 경우에는 1의 값을 가지며, 90°의 각을 이루면 0, 180°로 반대의 방향을 가지면 -1의 값을 갖게 됩니다. 즉, 결국 cosine 유사도는 -1 이상 1 이하의 값을 가지며 값이 1에 가까울수록 유사도가 높습니다.

문서 단어 행렬이나 TF-IDF 행렬을 통해서 문서의 유사도를 구하는 경우에는 문서 단어 행렬이나 TF-IDF 행렬이 각각의 특징 벡터 A, B가 됩니다.
-> EX)
문서1 : 저는 사과 좋아요
문서2 : 저는 바나나 좋아요
문서3 : 저는 바나나 좋아요 저는 바나나 좋아요
세 문서에 대해서 문서 단어 행렬을 만듭니다.

cosine 유사도를 구하는 함수를 구현하고 각 문서 벡터 간의 유사도를 계산해 보겠습니다.
import numpy as np
from numpy import dot
from numpy.linalg import norm
def cos_sim(A, B):
return dot(A, B)/(norm(A)*norm(B))
doc1 = np.array([0,1,1,1]) # 문서 단어 벡터
doc2 = np.array([1,0,1,1])
doc3 = np.array([2,0,2,2])
print('문서 1과 문서2의 유사도 :',cos_sim(doc1, doc2))
print('문서 1과 문서3의 유사도 :',cos_sim(doc1, doc3))
print('문서 2와 문서3의 유사도 :',cos_sim(doc2, doc3))
# 결과
문서 1과 문서2의 유사도 : 0.6666666666666667
문서 1과 문서3의 유사도 : 0.6666666666666667
문서 2와 문서3의 유사도 : 1.0000000000000002결과에서 중요한 점은 문서 1과 문서 2의 cosine 유사도와 문서1과 문서3의 cosine 유사도가 같다는 점과 문서2와 문서3의 cosine 유사도가 1이 나온다는 것입니다.
> 앞서 1은 두 벡터의 방향이 완전히 동일한 경우에 1이 나오며, cosine 유사도 관점에서는 유사도의 값이 최대임을 의미한다고 했습니다.
> 하지만 문서 3은 문서2에서 단지 모든 단어의 빈도수가 1씩 증가했을 뿐입니다. 다시 말해 한 문서 내의 모든 단어의 빈도수가 동일하게 증가하는 경우에는 기존의 문서와 cosine 유사도의 값이 1입니다.
-> 쓰일만한 곳
문서 A와 B가 동일한 주제의 문서, 문서 C는 다른 주제의 문서라고 해보겠습니다. 그리고 문서 A와 문서 C의 문서의 길이는 거의 차이가 나지 않지만, 문서 B의 경우 문서 A의 길이보다 두 배의 길이를 가진다고 가정하겠습니다.
> 이런 경우 유클리드 거리로 유사도를 연산하면 문서 A가 문서 B보다 문서 C와 유사도가 더 높게 나오는 상황이 발생할 수 있습니다.
> 이는 유사도 연산에 문서의 길이가 영향을 받았기 때문인데, 이런 경우 cosine 유사도가 해결책이 될 수 있습니다. cosine 유사도는 유사도를 구할 때 벡터의 방향(패턴)에 초점을 두므로 ★ cosine 유사도는 문서의 길이가 다른 상황에서 비교적 공정한 비교를 할 수 있습니다. ★
- 유사도를 이용한 영화 추천 시스템 구현
캐글에서 사용되었던 영화 데이터셋을 가지고 TF-IDF, cosine 유사도만으로 영화의 줄거리에 기반하여 영화를 추천!
> 여기서는 영화 제목과 줄거이로 유사도를 구할 것입니다. 좋아하는 영화를 입력하면 해당 영화의 줄거리와 유사한 줄거리의 영화를 추천하는 시스템 만드는 실습입니다.
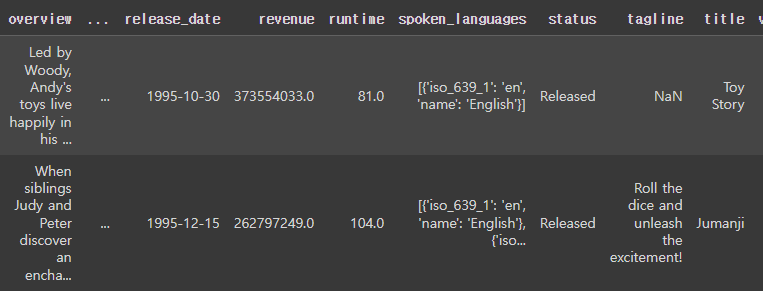
줄거리의 TF-IDF를 구해서 유사도를 구할 것입니다. TF-IDF는 NULL이 있으면 에러가 발생하니 결측치를 제거해야 합니다.
# overview 열에 존재하는 모든 결측값을 전부 카운트하여 출력
print('overview 열의 결측값의 수:',data['overview'].isnull().sum())
# 결과
overview 열의 결측값의 수: 135
# 결측값을 빈 값으로 대체
data['overview'] = data['overview'].fillna('')
=> TF-IDF 구하기
tfidf = TfidfVectorizer(stop_words='english')
tfidf_matrix = tfidf.fit_transform(data['overview']) # 이게 데이터 인덱스 순서로 들어가나봐
print('TF-IDF 행렬의 크기(shape) :',tfidf_matrix.shape)
# 결과
TF-IDF 행렬의 크기(shape) : (20000, 47487)TF-IDF 행렬의 크기는 20,000의 행을 가지고 47,847의 열을 가지는 행렬입니다. 다시 말해 20,000개의 영화를 표현하기 위해서 총 47,487개의 단어가 사용되었음을 의미합니다. 이것으로 cosine 유사도를 구할 수 있습니다.
cosine_sim = cosine_similarity(tfidf_matrix, tfidf_matrix) # 따라서 코사인 메트리스도 인덱스 순서로 들어가고
print('코사인 유사도 연산 결과 :',cosine_sim.shape)
# 결과
코사인 유사도 연산 결과 : (20000, 20000)무조건 정사각 모양입니다. 이는 20000개의 문서 벡터와 자기 자신을 포함한 20000개의 문서 벡터 간의 유사도가 기록되어 있습니다.(한 행에 하나의 문서와 다른 문서들과의 유사도가 다 기록되어 있는 것입니다.)
-> 유사도 구하기
title_to_index = dict(zip(data['title'], data.index))
# 영화 제목 Father of the Bride Part II의 인덱스를 리턴
idx = title_to_index['Toy Story']
print(idx)
# 결과
Toy story의 인덱스 0
title = "The Dark Knight Rises"
idx = title_to_index[title] # 다크나이트의 인덱스
sim_scores = list(enumerate(cosine_sim[idx]))
len(sim_scores)
# 결과
20000해당 영화와 모든 영화와의 유사도를 가져옵니다. -> 다크나이트와 다른 문서들간의 유사도는 1행 2만 열의 값이 있습니다.
# 유사도에 따라 영화들을 정렬한다.
sim_scores = sorted(sim_scores, key=lambda x: x[1], reverse=True)
# 가장 유사한 10개의 영화를 받아온다.
sim_scores = sim_scores[1:11]
# 가장 유사한 10개의 영화의 인덱스를 얻는다.
movie_indices = [idx[0] for idx in sim_scores]
# 가장 유사한 10개의 영화의 제목을 리턴한다. = fancy 인덱싱
data['title'].iloc[movie_indices]20000개를 정렬하고 10개의 영화를 추려서 fancy 인덱싱을 하면 됩니다. 중요한 것은 위에서 tf-idf 메트리스를 만들 때 데이터 원본 인덱스 그대로 들어가는 것 같습니다. 그래야만 iloc 할 때 idx로 접근할 수 있습니다.
- 여러가지 유사도 기법
1. 유클리드 거리
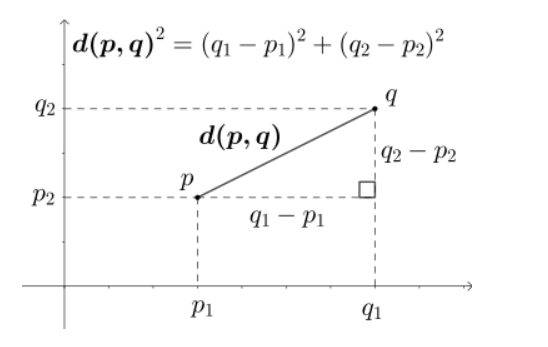
-> ex)
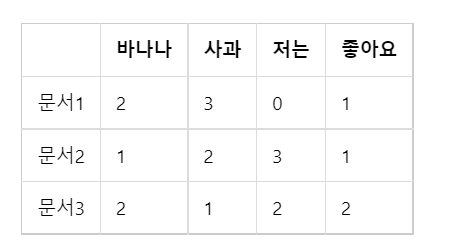
단어의 개수가 4개이므로 4차원 공간에 문서 1, 2, 3이 있습니다.
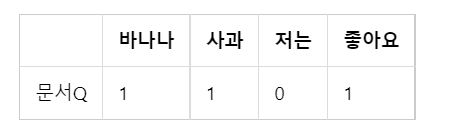
문서 Q가 문서 1, 2, 3 중 가장 유사한 문서를 찾고자 합니다. 그냥 Q와 다른 벡터와의 거리를 구하면 됩니다.
값이 작다는 것이 문서 간 거리가 가장 가깝다는 것을 의미합니다.
import numpy as np
def dist(x,y):
return np.sqrt(np.sum((x-y)**2))
doc1 = np.array((2,3,0,1))
doc2 = np.array((1,2,3,1))
doc3 = np.array((2,1,2,2))
docQ = np.array((1,1,0,1))
print('문서1과 문서Q의 거리 :',dist(doc1,docQ))
print('문서2과 문서Q의 거리 :',dist(doc2,docQ))
print('문서3과 문서Q의 거리 :',dist(doc3,docQ))
# 결과
문서1과 문서Q의 거리 : 2.23606797749979
문서2과 문서Q의 거리 : 3.1622776601683795
문서3과 문서Q의 거리 : 2.449489742783178
2. 자카드 유사도
A와 B 두개의 집합이 있다고 하면, 이때 교집합은 두 개의 집합에서 공통으로 가지고 있는 원소들의 집합을 말합니다. 즉, 합집합에서 교집합의 비율을 구한다면 두 집합 A와 B의 유사도를 구할 수 있다는 것입니다.
만약 두 집합이 동일하다면 1의 값을 가지고, 두 집합의 공통 원소가 없다면 0의 값을 갖습니다.
=> 순서
1) 문서 토큰화
doc1 = "apple banana everyone like likey watch card holder"
doc2 = "apple banana coupon passport love you"
# 토큰화
tokenized_doc1 = doc1.split()
tokenized_doc2 = doc2.split()
print('문서1 :',tokenized_doc1)
print('문서2 :',tokenized_doc2)
# 결과
문서1 : ['apple', 'banana', 'everyone', 'like', 'likey', 'watch', 'card', 'holder']
문서2 : ['apple', 'banana', 'coupon', 'passport', 'love', 'you']
2) 합집합 구하기
# 합집합
union = set(tokenized_doc1).union(set(tokenized_doc2))
print('문서1과 문서2의 합집합 :',union)
# 결과
문서1과 문서2의 합집합 : {'banana', 'holder', 'everyone', 'apple', 'passport', 'watch', 'love', 'you', 'coupon', 'card', 'like', 'likey'}
3) 교집합 구하기
# 교집합
intersection = set(tokenized_doc1).intersection(set(tokenized_doc2))
print('문서1과 문서2의 교집합 :',intersection)
# 결과
문서1과 문서2의 교집합 : {'banana', 'apple'}
-> 결과
print('자카드 유사도 :',len(intersection)/len(union))문서1과 문서2에서 둘 다 등장한 단어는 banana와 apple 총 2개입니다. 이제 교집합의 크기를 합집합의 크기로 나누면 자카드 유사도가 계산됩니다.
'[AI] > [네이버 BoostCamp | 학습기록]' 카테고리의 다른 글
| [22.04.27] 딥러닝 PART.CS231n 6강 (0) | 2022.12.27 |
|---|---|
| [22.01.19] 딥러닝 PART.CS231n 2강 (0) | 2022.12.27 |
| NLP PART.단어의 표현 (0) | 2022.12.24 |
| NLP PART.언어 모델 (0) | 2022.12.19 |
| NLP PART.텍스트 전처리2 (0) | 2022.12.19 |




