개발자로 후회없는 삶 살기
딥러닝 PART.교과목 오토인코더(Ae) 본문
서론
교과목 10주차 오토인코더에 관한 내용을 정리합니다.
본론
- 인-디코더라면?

encoding 과정은 입력 데이터를 가지고 잠재 공간상의 한 벡터로 변환하는 과정이 인코더의 역할입니다. > 디코더는 잠재 공간을 다시 출력 form으로 대응시켜 주는 것 > 잠재 공간을 feature map이라고 생각하면 됩니다.
- 활용

노이즈 영상을 입력으로 넣어서 노이즈를 제거하는 영상이 생성/ 해상도/ 복원(문화재)/ 과거의 흑백 영화를 컬러 영화로 바꾸기 시멘틱 분할 등등
- 유명한 네트워크
1. fcn(fully convolution netwokr)

dense가 없습니다. 모든 레이어가 conv로 되어있습니다. > 인코더는 vgg16으로 cnn 층입니다. = feature 뽑는 과정입니다. > 여기까지 줄이고 > 그 이후에 feature를 뽑았으니(encoding) encoding 정보를 토대로 분류기에 넣는 거였습니다. 그건 진짜 분류기 vgg 얘기고 > 분류기를 없애버리고 > vgg의 영상 분류기를 분류기 파트를 빼 버리고 디코더 파트를 넣은 것입니다. > 그때 skip 커넥션도 하고 transpose도 합니다. > 결과는 세그멘트 된 영상이 나옵니다.
2. Unet
- 오토 인코더

인-디코더인데 좀 특수한 목적으로 만들어졌습니다. > 인코더와 디코더는 반대로 뒤집은 대칭입니다. > 일반적으로 입력과 다른 출력을 얻으려고 하는 것이 인-디코더인데 얘는 입력 영상이 출력 영상으로 나온 결과물은 입력과 동일합니다. > reconstruction 재건했습니다. 새로 재건한 결과는 입력과 차이가 없도록 학습을 시킵니다. > 왜냐며? 인코더 디코더를 다 쓰겠다는 게 아니고 디코더는 필요 없고 인코더만 쓰기 때문입니다. > 인코더로 잠재 공간상의 원래 영상의 훨씬 더 사이즈가 적은 feature map을 얻을 수 있습니다.
+ 연구자가 처음에 "왜 재건 손실을 생각했을까"를 알 것 같습니다. 입력을 줄이고 줄여서 sigmoid해서 라벨과의 차이로 학습을 하는 거였는데 라벨이 사실 입력 이미지를 대표하는 것입니다. 그러니 라벨과 차이를 하지 말고 입력 이미지와 차이로 학습하자는 것으로 사실 같은 것입니다.
> 지금까지 feature map 뽑기는 cnn을 썼는데 분류하는 작업으로 학습을 시켜야 합니다. 오늘 이후로는 feature map 뽑기 cnn만 있는 게 아니라 오토인코더도 있다는 것을 알아야 합니다.
=> 특징
1. 입력 도메인과 출력 도메인이 동일합니다.
2. 잠재 공간 상 저 차원의 feature map 습득
3. 입력과 출력 간의 재건 손실을 최소화하도록 학습
4. 학습 후, 인코더를 입력 데이터의 차원 축소에 이용
★ 가장 큰 장점 : Ae는 라벨링 데이터가 필요 없습니다. self-supervised learning입니다. 인간이 라벨링을 해줄 필요가 없습니다. 영상만 있으면 됩니다. (이래서 gan도 쓰는 것 같습니다! 라벨이 필요가 없고 영상만 있으면 되고 1이다 0이다만 알려주면 되기 때문!)
=> 학습
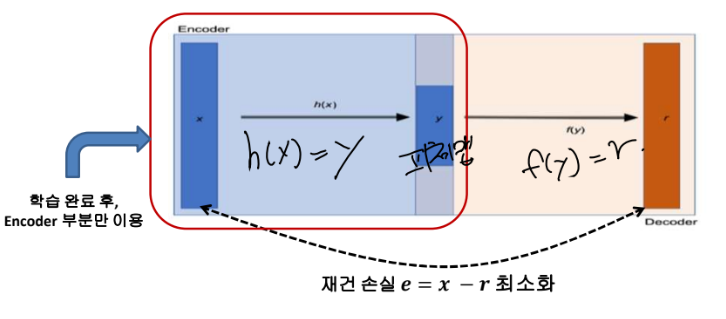
h가 encoding 전체 과정이고 r이 디코딩 전체 과정입니다. > 원래 이미지 x 와 출력 이미지의 r의 차로 학습을 해서 h와 r의 파라미터를 다 갱신하고 마지막에는 h만 써서 size가 작은 r을 뽑는 것을 사용합니다.
- vae
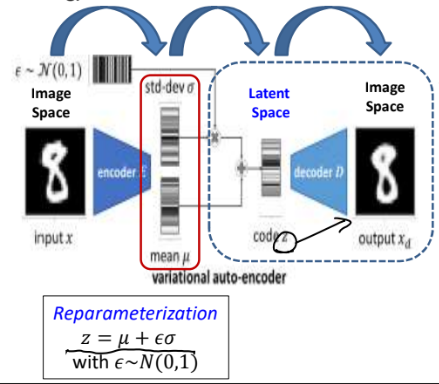
인코더가 달라집니다. > 디코더는 변동이 없고 z를 받아서 입력과 동일한 출력을 냅니다. > encoding은 두 번으로 이루어집니다. > 영상이 하나 들어오면 이 영상을 z 잠재 공간의 한 점(벡터)으로 대응시키는 게 아니고 어떤 분포로 대응을 합니다. 점들이 다다다다 찍혀 있는 것으로(확률분포) 대응시킵니다. > 그 분포는 평균과 분산이 있습니다. > 8을 받아서 한 점에 때리는 게 아니고 8이 속할 "이런 정도의 그룹에 너는 속할 것이다."라고 대응시킵니다. (그 그룹을 어떻게 표현할까요? 평균과 분산이 이러한 그룹에 대응시킵니다. = 평균과 분산으로 표현합니다.) > 인코더의 출력이 두 개의 벡터입니다. > 아까는 한 개인데 두 벡터가 밑에 있는 것은 평균이고 위가 분산입니다.

디코더는 분포로는 그림을 못 그립니다. 분포에서 한 점을 찍어줘야 (z가 필요) 그림을 그립니다. > 분포에서 한 점을 선택해야 하는데 그 과정이 reparameterization입니다. > z = 평균 + 분산(입실론) > 입실론을 샘플링합니다. (= 난수 발생해서) > 평균이 0이고 분산이 1인 분포에서 랜덤 샘플링합니다. > 그게 z이고 z가 디코더로 가서 영상을 만듭니다. > 이제 출력한 값과 입력 값의 차로 두 net를 학습합니다./
> 최종적으로는 마지막에 쓰는 주 목적은 디코더를 써서 새로운 영상을 만듭니다.
-> 손실

이때 손실은 인-디코더의 재건 손실과 + 인코더의 출력인 분포(평균, 분산)가 정규분포와 닮도록 정규분포와의 차이가 줄어들도록 손실을 정의합니다. (새로운 object가 추가되는 것입니다.)
'[AI] > [교과목 | 학습기록]' 카테고리의 다른 글
| [22.09.24] 딥러닝 PART.교과목(콜백, 모델 저장, tfds) (0) | 2022.12.27 |
|---|---|
| [22.09.14] 딥러닝 PART.교과목(퍼셉트론, 과적합 해소) (0) | 2022.12.27 |
| 딥러닝 PART.교과목 단어 임베딩 (0) | 2022.11.08 |
| 딥러닝 PART.교과목 RNN (0) | 2022.11.08 |
| 딥러닝 PART.교과목 transformer, BERT (0) | 2022.10.25 |




